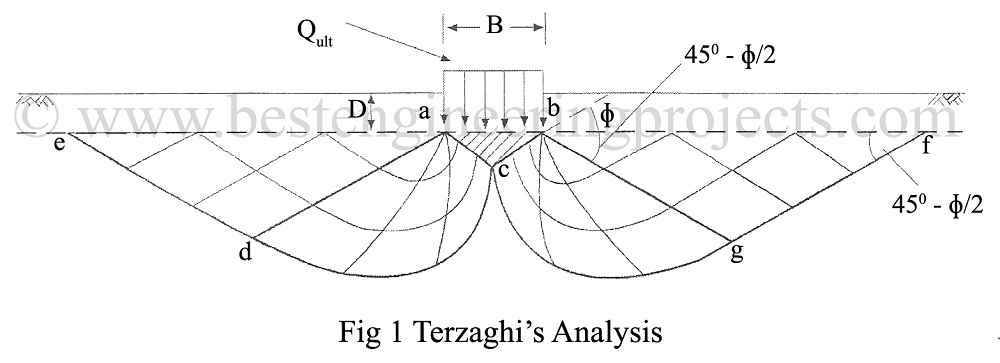
Terzaghi in 1943 gave a general bearing capacity theory for a strip foundation, called “Terzaghi’s Theory on Bearing Capacity Analysis“. For the first time, he developed his theory by incorporating the weight of the failure wedge in the analysis. Terzagi considered a continuous footing of width B placed at a depth of D below the ground surface as shown in fig.1.
In the derivation of the equation, the following assumptions were made.
- The soil is homogeneous, isotropic and Columb’s law of shear strength is valid.
- The footing is continuous and has a rough base.
- The failure zone does not extend above the base of the foundation.
- Shear resistance of the soil above the base of the foundation is neglected.
- The soil above the base of the foundation is replaced by a uniform surcharge.
- The principle of superposition holds good.
FAILURE MECHANISM | Terzaghi’s Theory on Bearing Capacity Analysis
The soil is assumed to fail along the surface aedcgfb. The failure surface consists of 5 zones. Zone I, abc is an elastic zone. Zone II, which comprises wedges beg and acd is the zone of radial shear, which is a transition from elastic to a plastic state. The wedges bfg and ade comprise Zone III and are known as passive Rankine’s zone and will be in a plastic state.
When the footing is loaded the wedge abc sinks into the ground as an integral part of the footing and remains in the elastic state due to the cohesion and adhesion between the base of the footing and the soil. The straight boundaries ac and bc of this zone are inclined at an angle with the base of the footing.
In Zones II and III, shear patterns develop. Zone II, the zone of radial shear constitutes a set of radial lines emerging from the outer edges b and a of the footing. The other set of lines in this zone are curves represented by log spiral. The equation of the log spiral is given by:
Where, r = the radius vector of the log spiral inclined at an angle to the initial radius vector r0, which is ac or bc.
The boundaries of passive Rankine’s Zone III are inclined at angles with the horizontal.
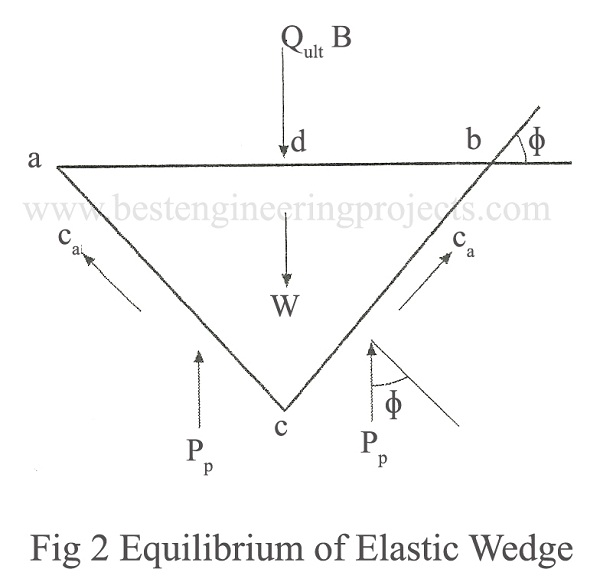
The ultimate bearing capacity Qult is obtained by considering the equilibrium of the elastic wedge in Zone I as shown in Fig.2. The Various forces acting on the Wedge are.
Pp = The resultant passive earth resistance at failure offered by the wedge bcgfb
Ca = Soil adhesion acting along with ac and bc
= Angle of internal friction
Qult = Ultimate bearing capacity
For equilibrium,
=
=
———- (1)
The passive force Pp is determined by considering the equilibrium of the passive wedge bcdeb. This is obtained by carrying out the three independent operations.
The operations comprise:
- Soil is assumed to have weight and possess no cohesion and surcharge.
- Soil is assumed to have surcharge only and possess no cohesion and weight.
- Soil is assumed to have cohesion only and possess no weight and surcharge.
With the above assumptions, the passive resistance , Ppq, and Ppc respectively due to weight, surcharge, and cohesion are determined and the values are superimposed. Hence, Pp can be written as:
———- (2)
Substituting the value of Pp in equation (1) we get,
———- (3)
———- (4)
———- (5)
———- (6)
———- (7)
———- (8)
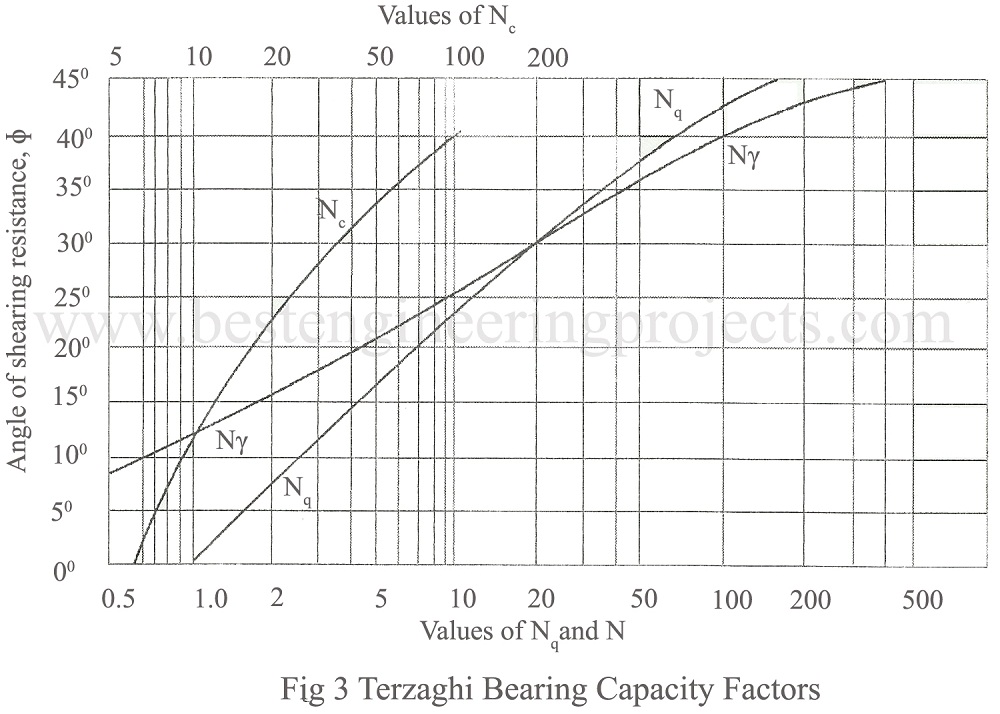
The factors , Nq, and Nc are called bearing capacity factors. These factors are functions of the angle of internal ɸ. The curve presented in Fig.3 below gives the bearing capacity factors for various values of the angle of internal friction
.
Safe Bearing Capacity
The safe bearing capacity is obtained as per the followings. Let Qnet be the net bearing capacity. The net bearing capacity, as per the definition is obtained as:
———- (9)
———- (10)
——— (11)
The limitation of Terzaghi’s theory is that it is applicable only for the shallow foundation. The theory has been derived for the case of general shear failure. For local shear failure, the following modification has been proposed by Terzaghi.
———- (12)
——— (13)
The reduction in shear parameters is due to the shear strength not being fully mobilized. The bearing capacity factors for use in general equation of Terzaghi should be based on the values of .
Limiting Condition for Local and General Shear Failure
| Parameters | General shear | Local shear |
| Strain | < 5% | 10 – 20% |
| >36 | <28 | |
| N Value | >30 | |
| Relative Density | >70% | < 35% |
| Void Ratio | <0.55 | >0.75 |
Bearing capacity for footing having limited dimension – The equation developed by Terzaghi is for strip foundation, which is considered as two-dimensional. The case of footings with finite dimensions is considered a three-dimensional problem. Based on experimental results Terzaghi suggested the following modifications for other footings such as square, circular, rectangular, etc.
Square Footing
———- (14)
Circular Footing
———- (15)
Rectangular Footing
———- (16)
More articles on Bearing Capacity Analysis posted on bestengineeringprojecs.com
- Bearing Capacity from in Situ Tests
- Hansen’s Bearing Capacity Theory
- Development of an equation of Bearing Capacity by Prandtl
- Bearing Capacity Analysis | Pauker – Rankine Method
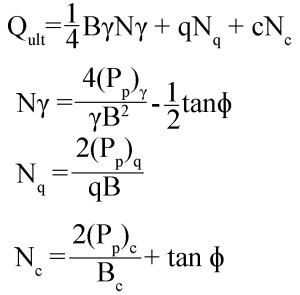
hi
Thank you